断层和折断线
本文的讨论和图形制作均基于 Surfer 13.x
断层和折断线的异同
相同的地方:
- 都是用来表示面上的不连续。
- 都用 Golden Software 的白化文件 [.bln] 格式来定义。
- 都要求网格足够密,否则效果不显。
不同之处:
- 断层就是把原本连续的面硬生生错断,所以断层本身没有 Z 值的概念。
- 折断线是在原本连续的面上建一堵墙,墙有高低起伏,所以折断线有 Z 值。
- 断层两侧的数据在网格化时,相互独立,互不干涉。
- 折断线两侧的数据在网格化时,同时参与,而且折断线本身的 Z 值也参与网格化。
再从图形直观感受:
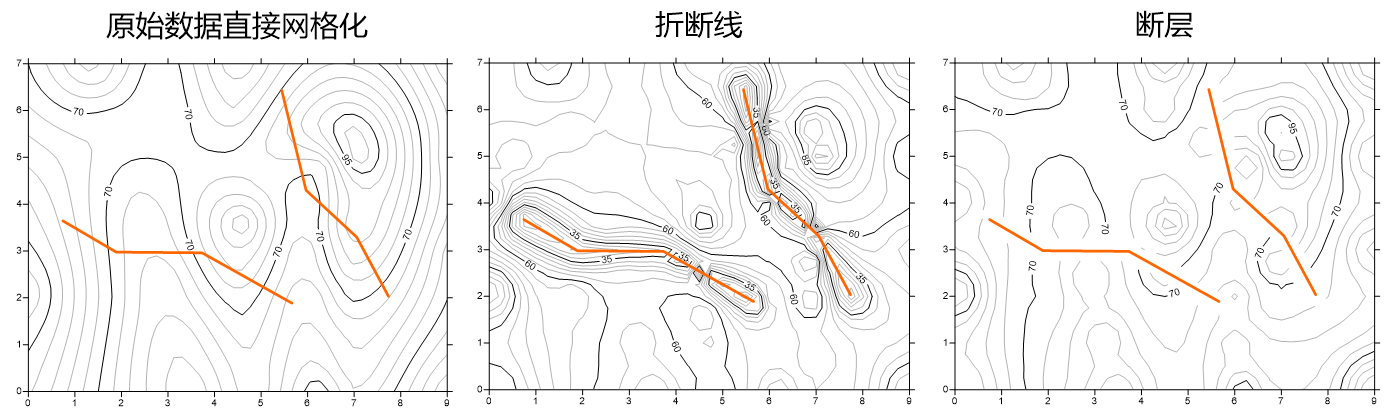
折断线
折断线的基本性质:
- 首先它是多段线。
- 线段上每个顶点都有对应的三维坐标(X, Y, Z)。
- 只能使用 .BLN 格式
当网格化方法发现有折断线时,会沿着折断线寻找最近点的 Z 值,并与附近点一起计算网格节点值。
Surfer 在网格化时,用且仅用线性插值方法来计算折断线顶点之间的值。
折断线并不能阻断信息的流通,所以网格化方法可以越过折断线,搜索到对面的数据。
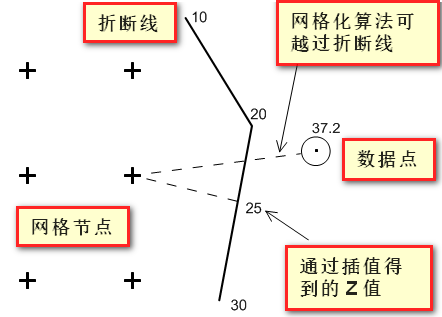
如果一个数据点刚好落在折断线上,那么折断线的值优先于它,也就是说,该数据点失效。
折断线可以用来表示河流、山脊、田垄、悬崖,以及等等。
网格化算法的搜索过程用到各向异性比率来检测折断线,所以,顶点多、复杂的折断线或者大量折断线存在,会显著降低网格化效能。
在制作折断线文件时,要注意,折断线不能与其他折断线或断层相交。
断层
断层也是一个多段线,但是其上每个顶点仅有二维坐标(X, Y)。
断层对信息流起阻断作用,断层一侧的数据并不能直接影响另一侧,需要“绕过”断层才能施加影响与另一侧(此时距离变大,影响因子变小)。
如果断层是一个封闭多边形,则无法被“绕过”,断层两侧分别网格化。
如果一个数据点刚好落在断层上,就通过一个随机修约误差检测来决定他属于哪一边。
断层极其耗费内存和网格化时间,大约与断层顶点数的平方成正比。
断层还可能导致某些网格化方法失败,例如最小曲率法,可能会因为不能收敛而失败。
只有 Surfer 7 以上版本的网格文件才能保存断层信息,低版本的网格文件会丢失断层信息,甚至断层本身被移除。
白化文件格式
白化文件 [.BLN] 用来表示边界信息,也常用来白化网格内的某些区域。
白化文件是逗号分隔的 ASCII 格式文件,可包含一个或多个多边形、多段线或点对象,每个对象都遵循以下格式:
| 格式 | 说明 |
|---|---|
| npts, flag | 对象的头信息;npts 表示紧跟着的顶点个数; flag 是白化标记,决定白化类型, 0 表示白化外部,1 表示白化内部。 |
| x1, y1 | 第一个顶点坐标 |
| x2, y2 | 第二个顶点坐标 |
| ... | 其他顶点坐标 |
| xn, yn | 最后一个顶点坐标。 如果此坐标与第一个坐标相同,表示该对象为封闭多边形。 |
多个多边形和多段线
一个白化文件内可以包含任意多的多边形和多段线对象,但是,有多个对象的白化文件用于白化时,文件内所有对象的 flag 值必须为 1 (Inside),否则会导致整个网格被白化。
如果要白化多个多边形的外部,必须将他们组合成一个复合多边形对象。
白化标记
白化标记参数(flag)用来决定白化内部(1)还是外部(0),怎么轻松区分 0 和 1 呢?1 和 Inside (内部)的首字母很像吧,看到 1 就想到 Inside,所以是白化内部;同理,0 和 Outside(外部) 的首字母很像,看到 0 就想到 Outside,白化外部。
如果白化文件用来表示折断线和断层,则白化标记参数无效,可以留空不填。
可选的 Z 坐标
目前而言,只有用作折断线时,才需要填 Z 值。
范例
假设要用 BLN 文件描述下面几个对象:
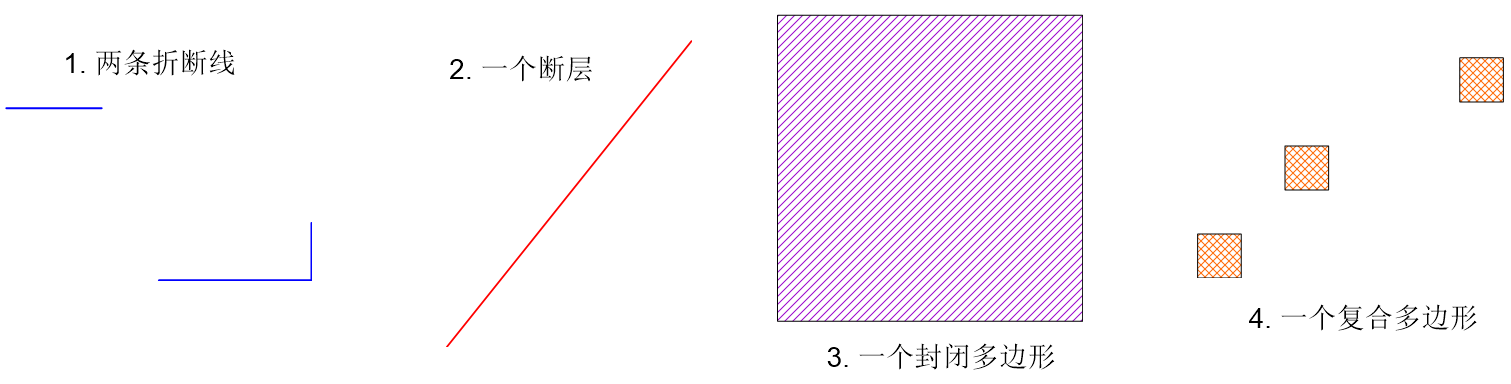
下面是两条折断线的例子,多段线对象的特点是,顶点超过一个(废话,一个顶点的对象就是点对象),起止坐标不同(相同就是封闭多边形了)。本例中,第一个对象有两个顶点,第二个对象有3个顶点:
2, 1
3.0, 4.5, 1.0
0.5, 4.5, 2.0
3, 1
4.5, 0.0, 1.1
8.5, 0.0, 1.2
8.5, 1.5, 1.4
下面是一条断层的例子,断层和折断线都是多段线对象,区别是断层没有 Z 值而折断线有:
2, 1
1.5, 1.0
7.5, 8.5
下面是一个封闭多边形的例子,多边形与多段线不同的地方就是,多边形的起止坐标相同:
5, 0
1.0, 1.0
1.0, 6.0
6.0, 6.0
6.0, 1.0
1.0, 1.0
下面是一个复合多边形的例子。复合多边形是什么玩意儿?复合多边形也是表示一个区域的对象,这个区域由超过一个多边形组成,但只保存为一个对象:
17, 0 <-- 由3个多边形组成的复合多边形
1, 1 <-- 第1个多边形的起点--原点(x1, y1)
1, 2
2, 2
2, 1 <-- 第1个多边形的终点
1, 1 <-- 重复原点(x1, y1)并闭合第1个多边形
3, 3 <-- 第2个多边形的起点
3, 4
4, 4
4, 3
3, 3 <-- 第2个多边形的终点,与其起点重合
1, 1 <-- 重复原点(x1, y1)
7, 5 <-- 第3个多边形的起点
7, 6
8, 6
8, 5
7, 5 <-- 第3个多边形的终点,与其起点重合
1, 1 <-- 重复原点(x1, y1),闭合整个复合多边形
复合多边形一般适合用作白化,不适合用于绘图。